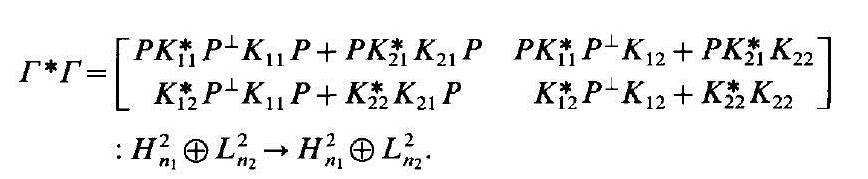Old research projects--but about to resurface
Aerospace

With
the return to the moon (Artemis project) and more urgently the national
security initiative in hypersonic technology [1], traditional aerospace
control, which had been overshadowed by such more "modern" applications
as Internet, power grid, biological, financial and so on control, is
resurfacing with an acute sense of emergency. Artificial Interlligence,
neural network control of hypersonic vehicles are likely to become
prolongations of hypersonic misile design optimization by genetic
algorithms as done in [1]: - E.
A. Jonckheere, P. Lohsoonthorn, S. Dalzell, ``Eigenstructure versus
constrained H-infinity design for hypersonic winged cone,'' Journal of Guidance, Dynamics and Control, American Institute of Aeronautics and Astronautics (AIAA), Vol. 24, No., 4, pp. 648-658, July-August 2001.
- E. A. Jonckheere, P. Lohsoonthorn, and S. K. Bohacek, ``From Sioux City to the X-33,'' (invited paper), Annual Reviews in Control, vol. 23, Elsevier, Pergamon, 1999, pp. 91-108, 1999.
- E.A. Jonckheere and G.-R. Yu, ``Propulsion control of crippled aircraft by H-infinity model matching,'' IEEE Transactions on Control Systems Technology, vol. 7, pp. 142-159, March 1999.
- E.A.
Jonckheere and G.-R. Yu,``H-infinity longitudinal control of crippled
trijet aircraft with throttles only,'' invited paper, IFAC Control Engineering Practice, vol. 6, No. 5, pp. 601-613, 1998.
- Ph.
C. Opdenacker, E.A. Jonckheere, M.G. Safonov, J.C. Juang and M. Lukich,
``Reduced order compensator design of a flexible structure," Journal of Guidance, Control and Dynamics, vol. 13, Number 1, pp. 46-56, January-February 1990.
Spectral theory of time-domain control operators
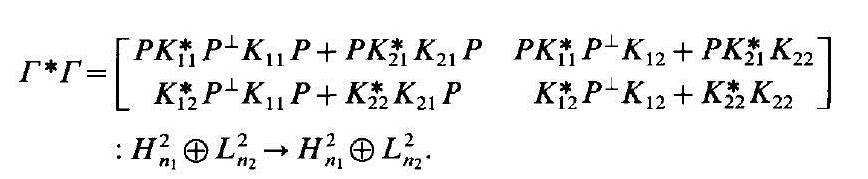
Robust
control design has traditionally been formulated in the
frequency-doamin, on the premise that a stabilized control system is a
frequency response to disturbances to be kept within identifiable
bounds under parameter variation. Time-domain transcriptions are
restricted to average or asymptotic responses. Fast switching quantum
gates, more generally quantum state transfer, usually entail
time-domain specifications, typically high fidelity, to be achieved
within a short amount of time.
Such specifications have their natural expression in the time-domain,
where the achievable performance is embedded in the spectrum of
Fredholm operators. This approach has its inception in the LQR problem
(see [8]). This old spectral theory is promising in a new domain of
applications--the spectral characterization of optimal fidelity and its
variation under paramete uncertainty. - Joseph A. Ball and Edmond A. Jonckheere, ``The four-block Adamjan-Arov-Krein Problem,'' Journal of Mathematical Analysis and its Applications, Volume 170, Number 2, pp. 322-342, November 1992.
- E.A.
Jonckheere, Jyh Ching Juang and Leonard M. Silverman, ``Spectral theory
of the linear quadratic and H-infinity problems," Linear Algebra and its Applications, Special Issue on Linear Systems and Control, vol. 122-123-124, pp. 273-300, September/October/November 1989.
- Jyh-Ching Juang and E.A. Jonckheere, ``On computing the spectral radius of the Hankel plus Toeplitz operator," IEEE Transactions on Automatic Control, vol. AC-33, pp. 1053-1059, November 1988.
- E.A.
Jonckheere and M. Verma, ``A spectral characterization
of H-infinity optimal feedback performance and its efficient
computation," Systems and Control Letters, vol. 8, pp. 13-22, October 1986.
- E.A. Jonckheere and L.M. Silverman, ``The linear-quadratic optimal control problem--the operator theoretic viewpoint," Operator Theory: Advances and Applications, Topics in Operator Theory Systems and Networks, vol. OT 12, Birkhauser Verlag, pp. 277-302, 1984.
- E.A.
Jonckheere and L.M. Silverman, ``Spectral theory of the
linear-quadratic optimal control problem: analytic factorization of
rational matrix-valued functions," SIAM Journal on Control and Optimization, vol. 19, pp. 262-281, March 1981.
- E.A. Jonckheere and L.M. Silverman, ``Spectral theory of the
linear-quadratic optimal control problem: a new algorithm for spectral
computations," IEEE Transactions on Automatic Control, vol. AC-25, pp.
880-888, October 1980.
-
E.A. Jonckheere and L.M. Silverman, ``Spectral theory of the
linear-quadratic optimal control problem: discrete-time single-input
case," IEEE Transactions on Circuits and Systems, Special Issue on Mathematical Foundation of Systems Theory, vol. CAS-25, pp. 810-825, September 1978.
Old research projects on dynamical systems, where the theory became reality--after 20 years
Dynamical
systems are ubiquitous in control, aerospace, celestian mechanics,
social networks, physiological systems, chaos and its various
manifestations. The latter led
us to consider tracking trajectories (periodic, aperiodic,
transitive, etc.) within the
attractor of a dynamical system with complicated (e.g., chaotic)
dynamics using linear quadratic (LQ) control of the the linear systems
modeling the deriation of the current trajectory from the nominal one.
Such linear systems are characterized by dynamically varying (as opposed to parameter varying) systems. Hence the phraseology Linear Dynamically Varying (LDV) control.
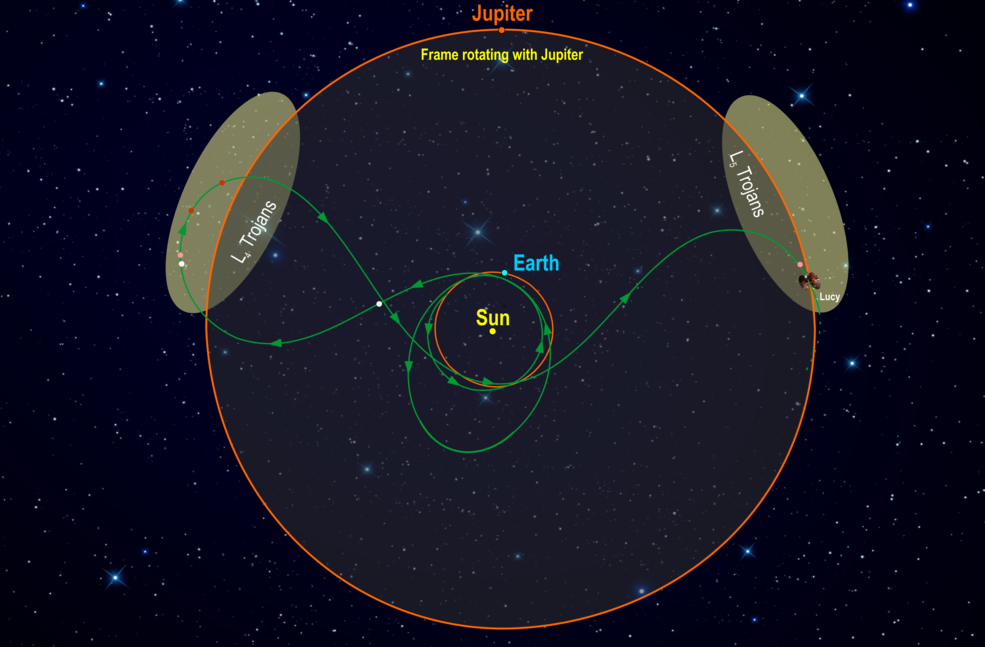
Already in [6], the possibility of using such technique in a
rendez-vous with the Giaccobini-Zinner comet was considered. Given that
the Trojan
asteroids in the Lagrange L4 point offer a perfect example of a chaotic
attractor, back in 2003, an LDV controller was theoretically designed
to send
a spacecraft to a rendez-vous with a Trojan asteroid [2]. Twenty years
later,
the Lucy spacecraft of NASA will make a flyby by the Lagrange L4 point
of the Sun-Jupiter system.
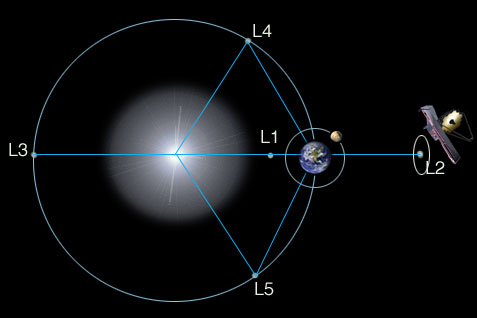
Even
more recently, the James Webb telescope has been "parked" at the L2
point
of the Sun-Earth system because of its (marginal) stability property.
Overall, the Lagrange points offer tremendous possibilities for space
exploration.

- E. Jonckheere and S. Bohacek, ``Linear Dynamically Varying (LDV) control over compact Riemannian manifolds,'' 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, December 15-17, 2010, pp. 7099-7104.
- F.
Ariaei, E. Jonckheere and S. Bohacek, ``Tracking Trojan asteroids in
periodic and quasi-periodic orbits around the Jupiter Lagrange point
using LDV techniques,'' Physics and Control, St. Petersbourg, Russia, August 21-23, 2003, pp. 101--106.
- Stephan Bohacek and Edmond Jonckheere, ``Relationship between linear dynamically varying systems and jump linear systems,'' Mathematics of Control, Signals, and Systems(MCSS), vol. 16, pp. 207-224, 2003.
- S. Bohacek and E. A. Jonckheere, ``Structural stability of linear dynamically varying (LDV) controllers,'' Systems and Controls Letters (SCL), volume 44, pp. 177-187, 2001.
- S. Bohacek and E. A. Jonckheere, ``Nonlinear tracking over compact sets with Linear Dynamically Varying H-infinity control,'' SIAM J. Control and Optimization, vol. 40, No. 4, pp. 1042-1071, 2001.
- S. Bohacek and E. A. Jonckheere, ``Linear Dynamically Varying LQ control of nonlinear systems over compact sets,'' IEEE Transaction on Automatic Control, volume 46, pp. 840-852, June 2001.
- S.
Bohacek and E. Jonckheere, "Analysis and synthesis for linear
set-valued dynamically varying systems," Proceedings of the 2000
American Control Conference. ACC (IEEE Cat. No.00CH36334), 2000, pp.
2770-2774 vol.4, doi: 10.1109/ACC.2000.878714.
Latest news: US Space Force initiative on Security of Cis-Lunar Space
With
the Artenis return-to-the-moon project and stiffening international
competition for presence in cis-lunar space, securing this space has
become a national priority. Navigation among the Lagrange points of the
Earth-Monn system is reminiscent of our early project of navigating
around the L4 point of the Jupiter-Sun system.